算法思路及技巧
二分法
- 只要看到面试题里给出的数组是 有序数组,都可以想一想是否可以使用二分法。
- 同时题目还强调数组中 无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的。
正常二分
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1, 0, 3, 5, 9, 12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1, 0, 3, 5, 9, 12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
题解:
class Solution(object):
def search(self, nums, target):
left = 0
right = len(nums)
while left < right:
mid = (left + right) // 2
if nums[mid] > target:
right = mid
elif nums[mid] < target:
left = mid + 1
else:
return mid
return -1
class Solution(object):
def search(self, nums, target):
left = 0
right = len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] > target:
right = mid - 1
elif nums[mid] < target:
left = mid + 1
else:
return mid
return -1
边界二分
当题目中存在重复元素时,使用二分查找法返回指定元素的左边界或者右边界。
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5, 7, 7, 8, 8, 10], target = 8
输出:[3, 4]
示例 2:
输入:nums = [5, 7, 7, 8, 8, 10], target = 6
输出:[-1, -1]
示例 3:
输入:nums = [], target = 0
输出:[-1, -1]
题解:
class Solution:
def get_left_border(self, nums, target):
left = 0
right = len(nums) - 1
left_border = -2 # 当 target 比所有数都小
# 正常情况下用 -1 但是这里当target 比所有数都小的时候 left_border 也会等于 -1
while left <= right:
mid = (left + right) // 2
if nums[mid] >= target: # 得出的数会在 target 的左边边一个
right = mid - 1
left_border = right
else:
left = mid + 1
return left_border
def get_right_border(self, nums, target):
left = 0
right = len(nums) - 1
right_border = -2 # 当 target 比所有数都大
while left <= right:
mid = (left + right) // 2
if nums[mid] <= target: # 得出的数会在 target 的右边一个
left = mid + 1
right_border = left
else:
right = mid - 1
return right_border
def search_range(self, nums: List[int], target: int) -> List[int]:
left_border = self.get_left_border(nums, target)
right_border = self.get_right_border(nums, target)
print(left_border, right_border)
if left_border == -2 or right_border == -2:
return [-1, -1]
if right_border - left_border > 1: # 因为一左一右所以是">1"
return [left_border + 1, right_border - 1]
return [-1, -1]
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder = getLeftBorder(nums, target);
int rightBorder = getRightBorder(nums, target);
if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
return {-1, -1};
}
private:
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int rightBorder = -2;
while (left <= right) {
int mid = left + ((right - left) / 2); // 防止溢出 等同于(left + right)/2
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
rightBorder = left;
}
}
return rightBorder;
}
int getLeftBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int leftBorder = -2;
while (left <= right) {
int mid = left + ((right - left) / 2);
if (nums[mid] >= target) {
right = mid - 1;
leftBorder = right;
} else {
left = mid + 1;
}
}
return leftBorder;
}
}
双指针
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新数组下标的位置
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组、链表、字符串等操作的面试题,都使用双指针法。
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
注意: 如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:s = "ab#c", t = "ad#c"
输出:true
解释:s 和 t 都会变成 "ac"。
示例 2:
输入:s = "ab##", t = "c#d#"
输出:true
解释:s 和 t 都会变成 ""。
示例 3:
输入:s = "a#c", t = "b"
输出:false
解释:s 会变成 "c",但 t 仍然是 "b"。
题解:
class Solution:
def backspaceCompare(self, s: str, t: str) -> bool:
p, k = 0, 0
s = list(s)
t = list(t)
for i in range(len(s)):
if s[i] == '#' and p > 0:
p -= 1
elif s[i] != '#': # 注意这里当 如果不写当 != '# 且 p>0 时会将 '#' 加进来
s[p] = s[i]
p += 1
for i in range(len(t)):
if t[i] == '#' and k > 0:
k -= 1
elif t[i] != '#':
t[k] = t[i]
k += 1
return s[:p] == t[:k]
class Solution:
def backspaceCompare(self, s: str, t: str) -> bool:
stack_s = []
stack_t = []
for i in s:
if i != '#':
stack_s.append(i)
else:
stack_s.pop() if len(stack_s) > 0 else ...
for j in t:
if j != '#':
stack_t.append(j)
else:
stack_t.pop() if len(stack_t) > 0 else ...
return stack_s == stack_t
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
实现滑动窗口,主要确定以下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] 并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2, 3, 1, 2, 4, 3]
输出:2
解释:子数组 [4, 3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1, 4, 4]
输出:1
示例 3:
输入:target = 11, nums = [1, 1, 1, 1, 1, 1, 1, 1]
输出:0
题解:
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
j, ans, sum_ = 0, float('inf'), 0
for i in range(len(nums)):
sum_ += nums[i]
while sum_ >= target: # 等于也要
sub_len = i - j + 1
ans = min(sub_len, ans)
sum_ -= nums[j]
j += 1
return ans if ans != float('inf') else 0
模拟
边界条件非常多时,在一个循环中,需要按照固定规则来遍历。这就是 循环不变量原则。
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3
输出:[[1, 2, 3], [8, 9, 4], [7, 6, 5]]
示例 2:
输入:n = 1
输出:[[1]]
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
题解:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
startx, starty = 0, 0
loop = n // 2
offset = 1
count = 1
ans = [[0] * n for _ in range(n)]
while loop:
x, y = startx, starty
while x < n - offset:
ans[y][x] = count
x += 1
count += 1
while y < n - offset:
ans[y][x] = count
y += 1
count += 1
while x > startx:
ans[y][x] = count
count += 1
x -= 1
while y > starty:
ans[y][x] = count
count += 1
y -=1
offset += 1
loop -= 1
startx += 1
starty += 1
if n & 1: # 奇数需要单独画中间部分
ans[n // 2][n // 2] = n ** 2
return ans
虚拟节点
在链表中移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。为了不单独写一段逻辑(将头结点向后移动一位)来处理移除头结点的情况,可以设置一个虚拟头结点,这样原链表的所有节点就都可以按照统一的方式进行移除了。
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
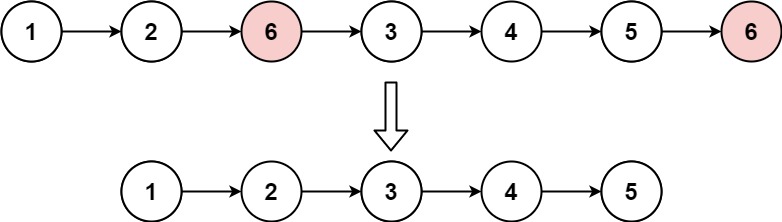
输入:head = [1, 2, 6, 3, 4, 5, 6], val = 6
输出:[1, 2, 3, 4, 5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7, 7, 7, 7], val = 7
输出:[]
题解:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
if head == None: return None
dummy = ListNode(next = head)
cur = dummy
while cur.next:
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return dummy.next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
if head == None: return None
dummy = ListNode(-1)
dummy.next = head
p = dummy
cur = head
while cur:
if cur.val == val:
p.next = cur.next
cur = p.next
else:
p = cur
cur = p.next
return dummy.next
哈希表
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。但是哈希法也是 牺牲了空间换取了时间,因为我们要使用额外的数组,set 或者是 map 来存放数据,才能实现快速的查找。
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法!
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:
若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
题解:
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
map = [0] * 26
for i in s:
map[ord(i) - ord('a')] += 1
for i in t:
map[ord(i) - ord('a')] -= 1
for i in map:
if i != 0:
return False
return True
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
s_dic = defaultdict(int)
t_dic = defaultdict(int)
for i in s:
s_dic[i] += 1
for i in t:
t_dic[i] += 1
return s_dic == t_dic
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
s_dic = Counter(s)
t_dic = Counter(t)
return s_dic == t_dic
defaultdict 和 Counter 都来自 collections 模块,下面是一些关于 collections 的介绍(有机会的话可单独一篇来介绍):
官方说法:
collections 模块实现了特定目标的容器,以提供Python标准内建容器dict、list、set 和 tuple 的替代选择。
通俗说法:
Python 内置了一些数据类型和方法,collections 模块在这些内置类型的基础提供了额外的高性能数据类型,比如基础的字典是不支持顺序的,collections 模块的 OrderedDict 类构建的字典可以支持顺序。collections模块的这些扩展的类用处非常大,熟练掌握该模块,可以大大简化Python代码,提高Python代码逼格和效率,高手入门必备。
KMP
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
class Solution:
def getnext(self, next, s):
j = -1
next[0] = j
for i in range(1, len(s)):
while j >= 0 and s[i] != s[j + 1]:
j = next[j]
if s[i] == s[j + 1]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if not needle:
return 0
next = [0] * len(needle)
self.getnext(next, needle)
j = -1
for i in range(len(haystack)):
while j >= 0 and haystack[i] != needle[j + 1]:
j = next[j]
if haystack[i] == [j + 1]:
j += 1
if j == len(needle) - 1:
return i - len(needle) + 1
return -1
栈
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
题解:
class Solution:
def isValid(self, s: str) -> bool:
map_dic = {']':'[', '}':'{', ')':'('}
stack =[]
for i in s:
if i in map_dic.values():
stack.append(i)
else:
if not stack:
return False
if stack[-1] != map_dic[i]:
return False
stack.pop()
if stack:
return False
return True
队列
单调队列
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。实现的单调队列不是对数组里面的数进行排序。 单调队列中维护的是有可能成为窗口里最大(最小)值的元素就,同时保证队列里的元素数值是由大到小(小到大)的。
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1, 3, -1, -3, 5, 3, 6, 7], k = 3
输出:[3, 3, 5, 5, 6, 7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
题解:
from collections import deque
class MyQueue(): # 创建单调队列
def __init__(self):
self.que = deque()
def push(self, val):
while self.que and val > self.que[-1]:
self.que.pop()
self.que.append(val)
def pop(self, val):
if self.que and val == self.que[0]:
self.que.popleft()
def front(self):
return self.que[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
for i in nums[:k]: # 创建窗口
que.push(i)
ans = []
ans.append(que.front()) # 将第一个窗口中的值保存到结果中
for i in range(k, len(nums)): # 移动窗口
que.pop(nums[i - k]) # 移除左边的数
que.push(nums[i]) # 加入右边的数
ans.append(que.front()) # 获取最大值
return ans
优先队列
优先对列就是一个披着队列外衣的堆。
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1, 1, 1, 2, 2, 3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
题解:
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
map_dic = dict()
for i in nums:
map_dic[i] = map_dic.get(i, 0) + 1
que = []
for key, n in map_dic.items():
heapq.heappush(que, (n, key))
if len(que) > k:
heapq.heappop(que)
ans = []
for i in que:
ans.append(i[1])
return ans
